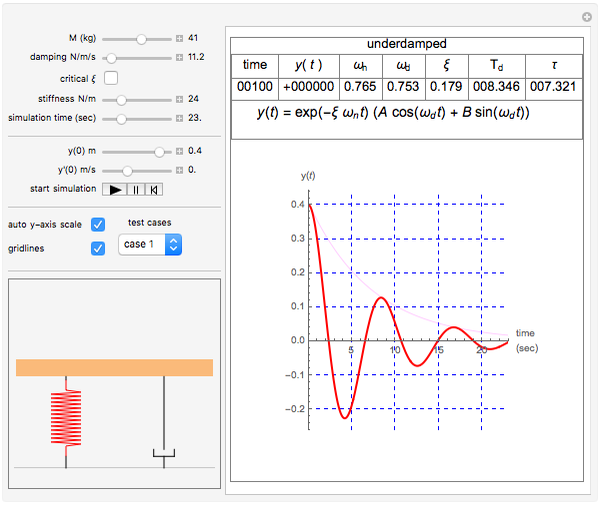
Underdamped Second Order System
Graphical Method Second Order Underdamped Dynamics And Control
Underdamped second order system. General case for a second-order system. Underdamped second-order system Posted by lftourviajes on November 14 2017 Posted in. Effects of Gain ζ and ω 0 on Second Order Lowpass Step Response.
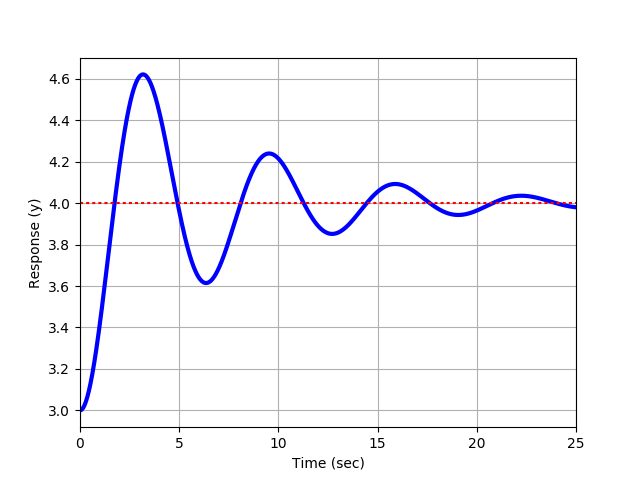
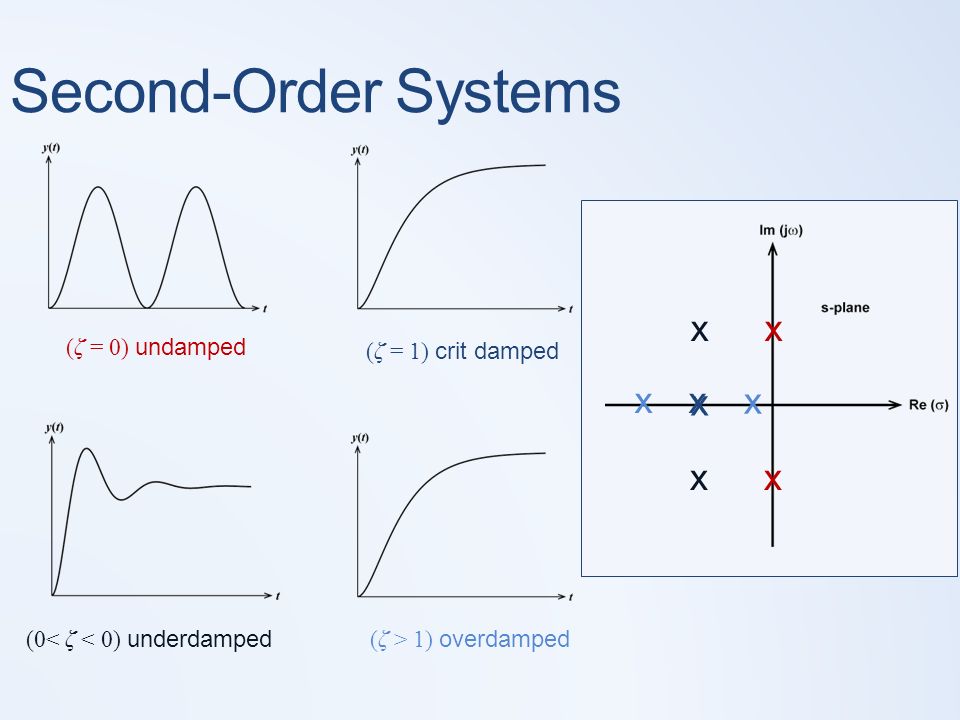
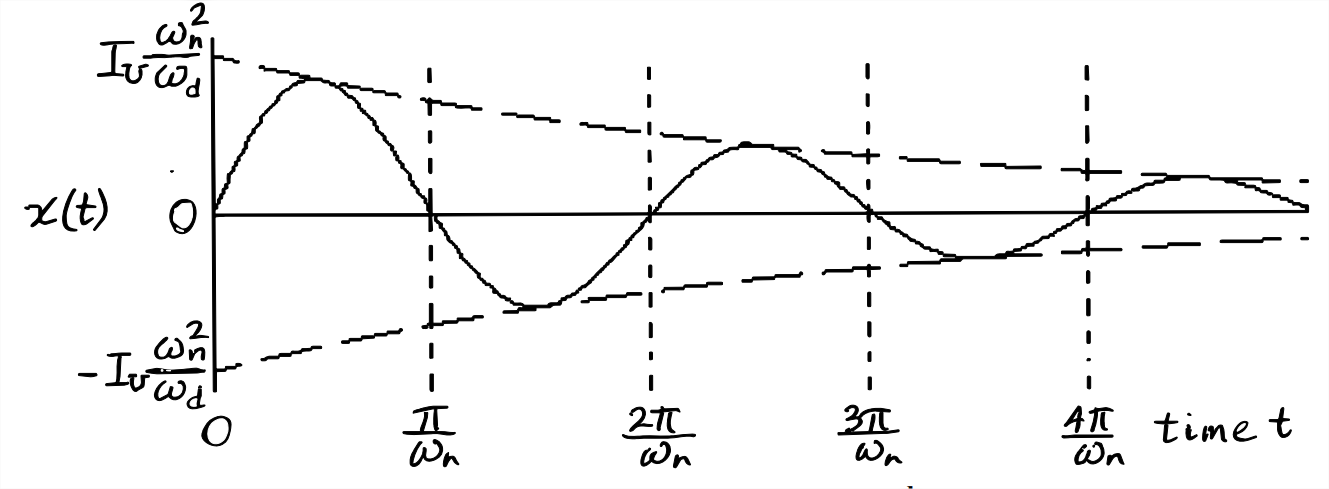
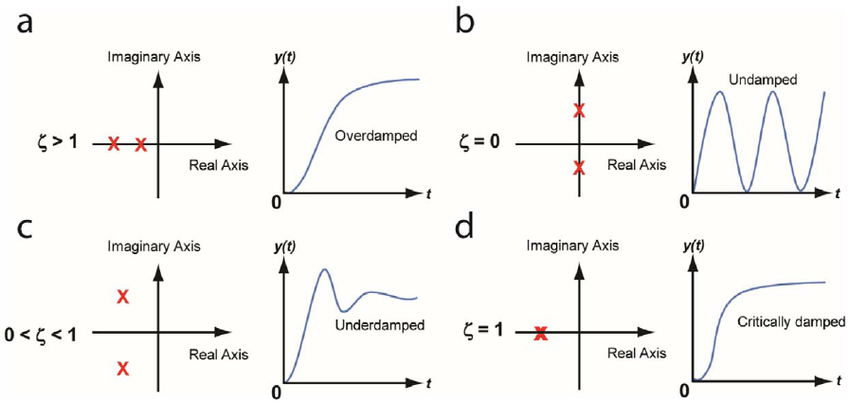
So xt et2 cos 11 t2 1 11 sin 11 t2 12 et2 11 cos 11 t2 φ where φ tan11 11. Underdamped case results in complex numbers This generates a decaying oscillating case. The more common case of 0 1 is known as the under damped system.
This corresponds to ζ 0 and is referred to as the undamped case. Now If δ 1 the two roots s 1 and s 2 are real and we have an over damped system. A conservative system without viscous dissipation the roots of the characteristic equation are imaginary.
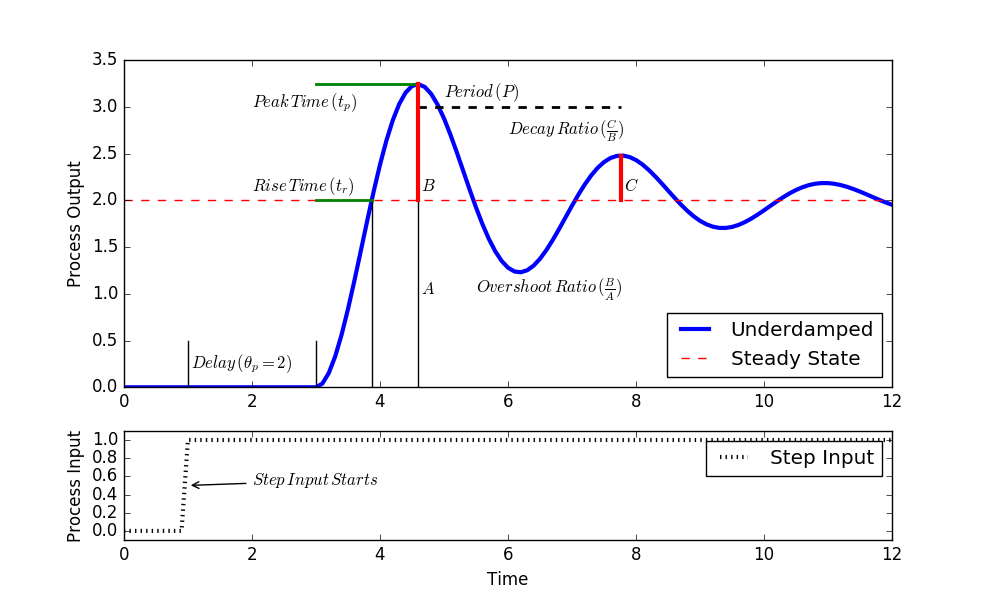
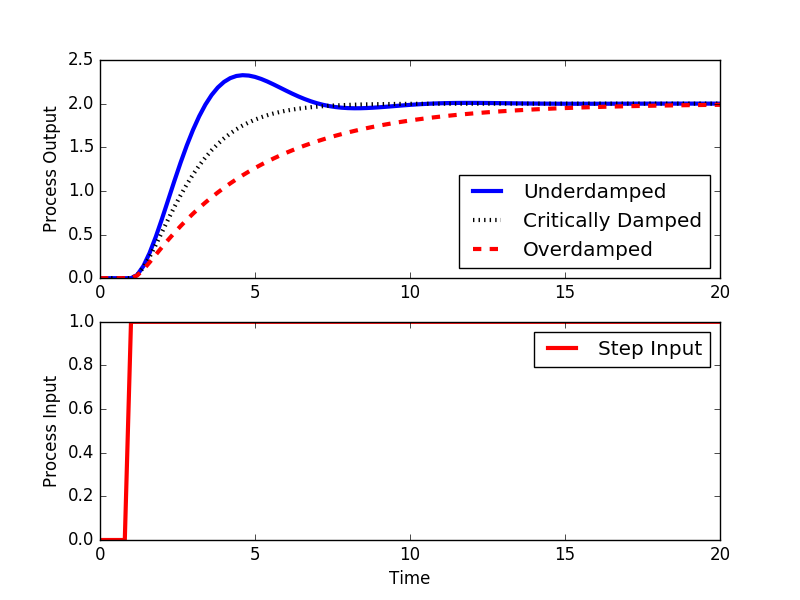
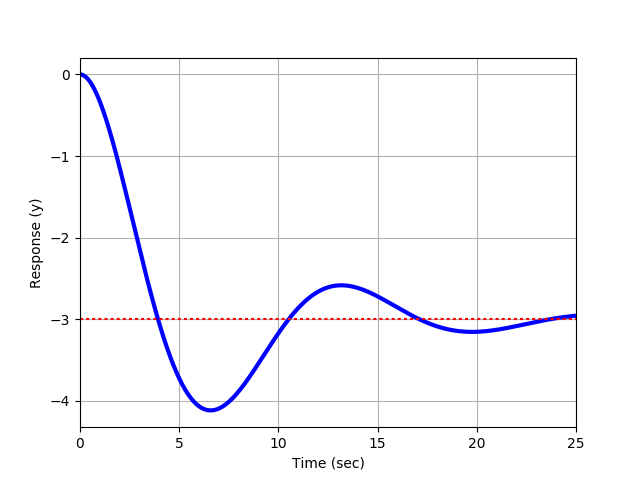
Calculate τ s τ s from equations for rise time tr t r peak time tp t p or. The response depends on whether it is an overdamped critically damped or underdamped second order system. Second order systems may be underdamped critically damped overdamped or unstable.
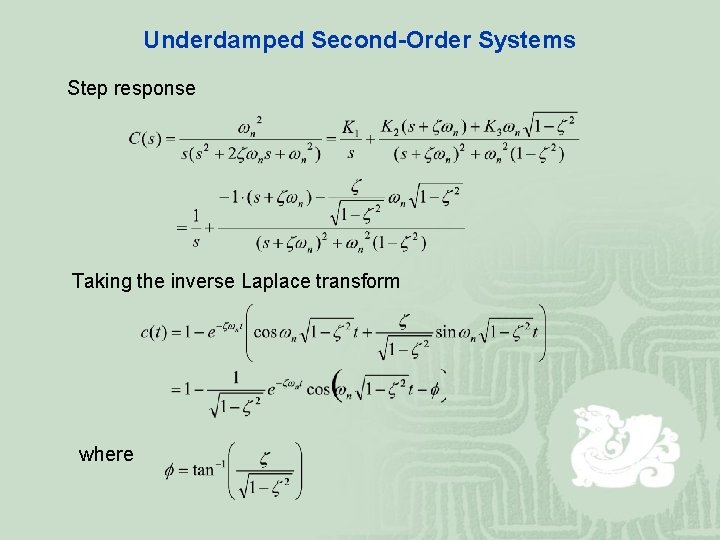
Calculate Kp Δy Δu K p Δ y Δ u. The new aspects in solving a second order circuit are the possible forms of natural solutions and the requirement for two independent initial conditions to resolve the unknown coefficients. The pole locations of the classical second-order homogeneous system d2y dt2 2ζωn dy dt ω2 ny0 13 described in Section 93 are given by p1p2 ζωn ωn ζ2 1.
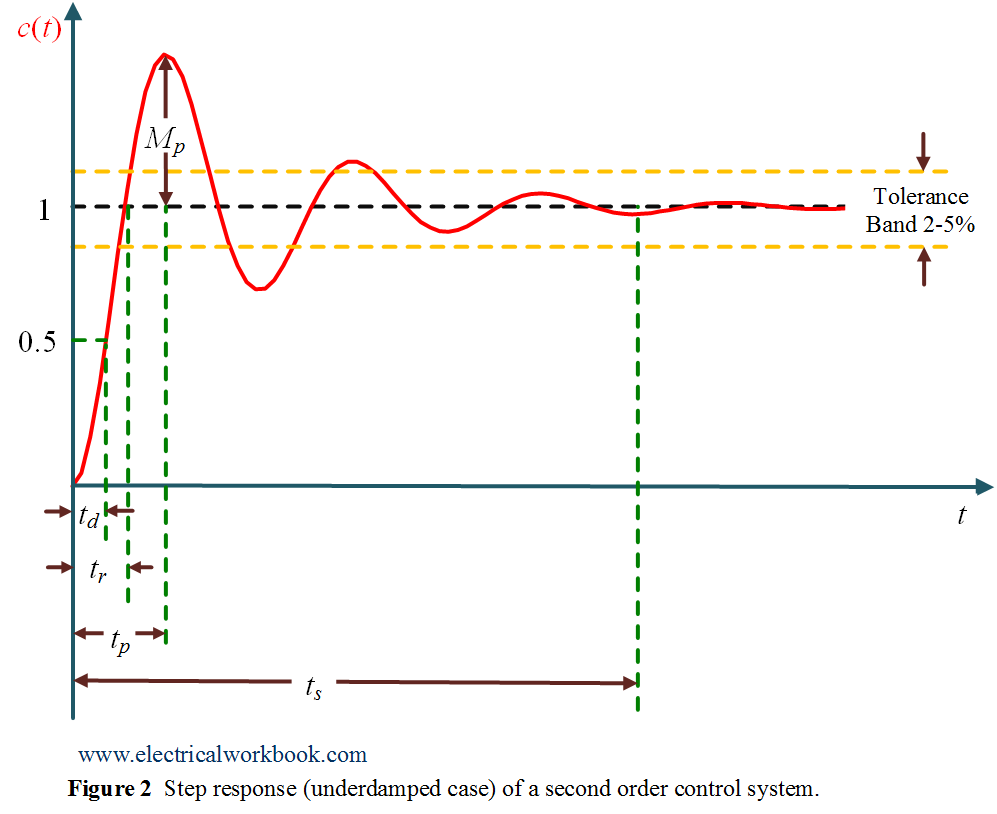
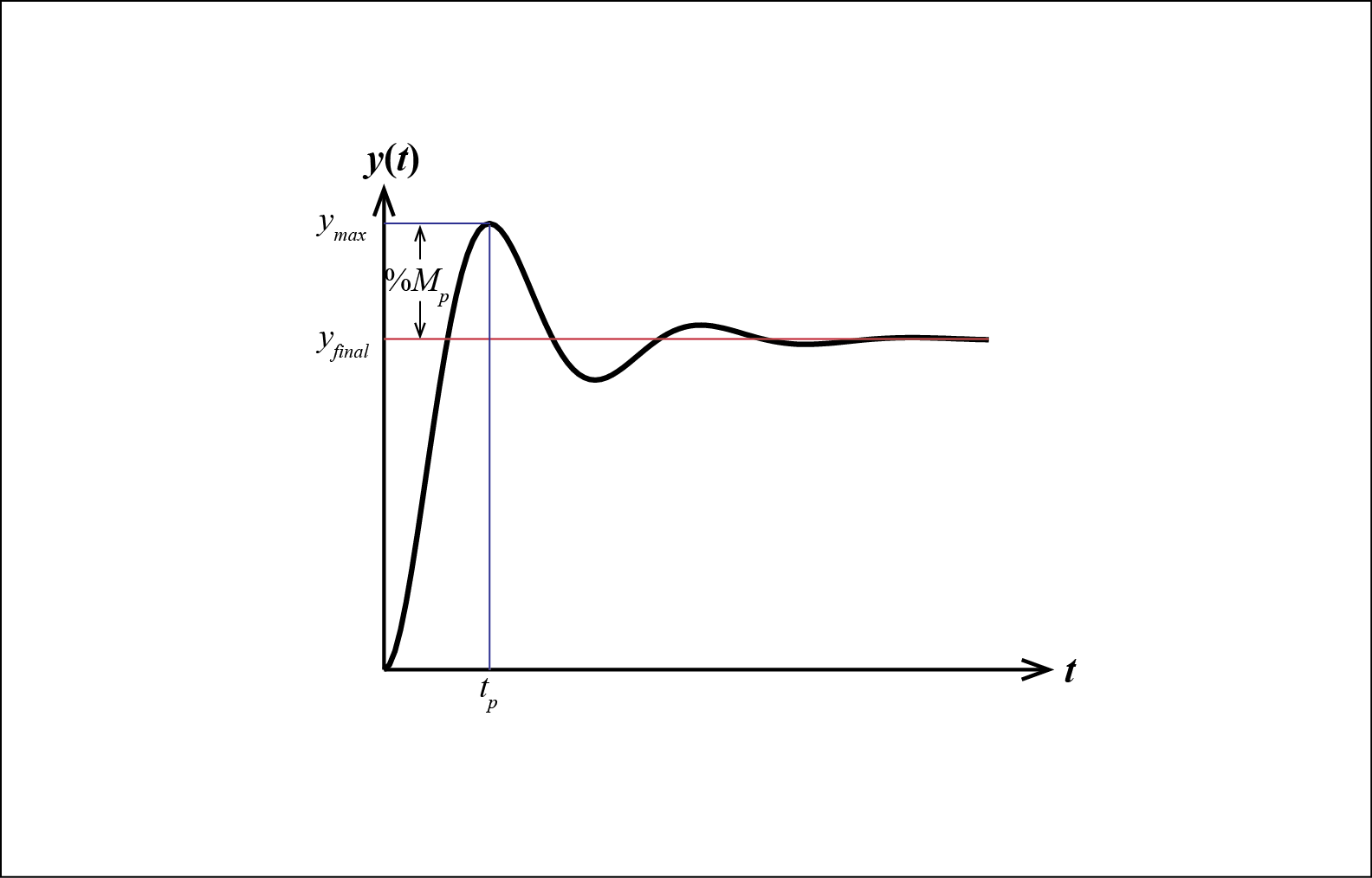
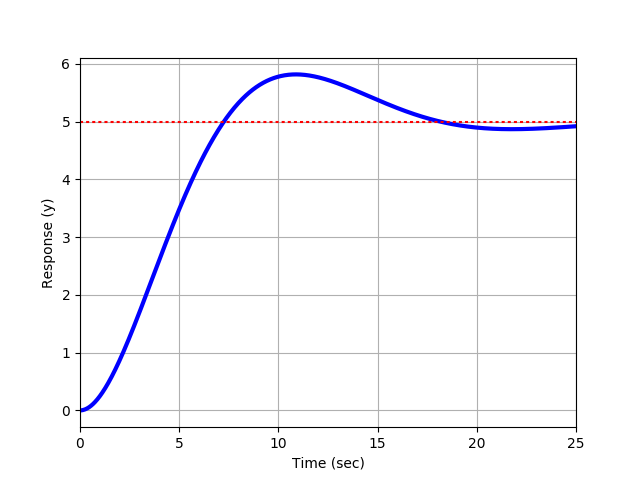
Xt K1t exp s1t K2 exp s2t. Peak time in step response underdamped case of a second order control system.
If b2 4mk 0 then the poles are complex conjugates lying in the left half of the s-plane. A second-order system in standard form has a characteristic equation s2 2 ζωns ωn2 0 and if ζ 0 the system is underdamped and the poles are a complex conjugate pair.
Second Order Systems Dynamics And Control
Underdamped Second Order System Example Youtube
Underdamped Second Order System Dademuchconnection
Graphical Method Second Order Underdamped Dynamics And Control
Underdamped Second Order System Dademuchconnection
File Second Order Under Damped Response Svg Wikimedia Commons
Unit Step Response For Underdamped Second Order Systems Download Scientific Diagram
Graphical Method Second Order Underdamped Dynamics And Control
Second Order Underdamped Transfer Functions Youtube
Help
Peak Overshoot In Step Response Underdamped Case Of A Second Order Control System Electricalworkbook
Second Order Underdamped Response Specifications Download Scientific Diagram
Second Order Systems Part I Boing Jason Sachs
Time Delay Of An Underdamped Second Order System Titanlab Org
How Do I Tell The Difference Between 1st Order Response And 2nd Order Response Mathematics Stack Exchange
5 Response Of An Underdamped General Second Order Transfer Function To Download Scientific Diagram
The Unit Step Response
11 Impulse Response Of The Second Order Underdamped Systems Download Scientific Diagram
Lecture 13 Second Order Systems Time Response Lecture 12 First Order Systems Lecture 13 Second Order Systems Lecture 14 Non Canonical Systems Me 431 Ppt Download
Time Response Of Second Order Control System Worked Example Electrical4u
Control Tutorials For Matlab And Simulink Introduction System Analysis
9 7 Ideal Impulse Response Of Underdamped Second Order Systems Engineering Libretexts
File Second Order Under Damped Response Svg Wikimedia Commons
1
Second Order Systems In Process Control Youtube
Typical Step Response Of An Underdamped Second Order System Download Scientific Diagram
Solved Problem Description Use A Script To Identify The Chegg Com
Bode Plot For Underdamped 2nd Order System Bode Plots For Flickr
Graphical Method Second Order Underdamped Dynamics And Control
Step Response Of A Second Order System With Respect To The Damping Download Scientific Diagram
Solved Consider Three Underdamped Second Order Systems One Chegg Com
2
Transient Response Of Second Order Control System Youtube
Control Tutorials For Matlab And Simulink Introduction System Analysis
Solved For The Second Order Under Damped System Shown Below Chegg Com
Graphical Method Second Order Underdamped Dynamics And Control
11 Normalized Frequency Response Of A Second Order Underdamped System Download Scientific Diagram
Chapter 5
Approximation Of Magnitude And Phase Of Underdamped Second Order Systems
Step And Impulse Response Of A Second Order System Wolfram Demonstrations Project
Free Response In A Second Order System Wolfram Demonstrations Project
Time Domain Specifications
Transient Time Response Of A Second Order Underdamped System With 0 D Damping Ratio 1
2
Control System Time Response Of Second Order System Javatpoint
Underdamped Second Order System Dademuchconnection
Gate Ese Impulse And Step Response For Second Order System Offered By Unacademy
Out Response Poles And Zeros The Output Response
1
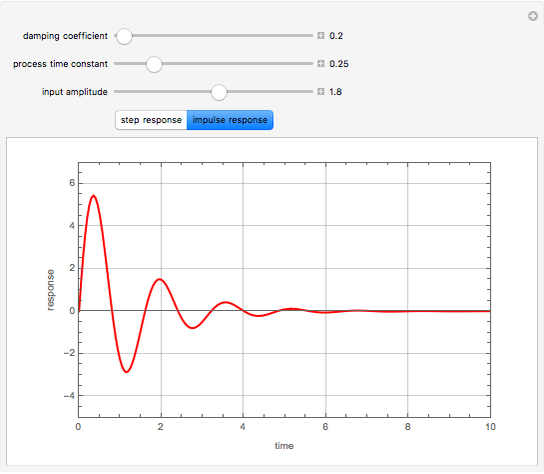
This example problem demonstrates how to analyze an underdamped system t.
SECOND-ORDER SYSTEMS 29 First if b 0 the poles are complex conjugates on the imaginary axis at s1 j km and s2 j km. The initial conditions are satisfied when c 1 1 and c 2 1 11. The roots for this system are. 4 Critically Damped The unit step response of a critically damped system ζ1 with zero initial conditions is given by xt 1 1 e 1 t n t 2 n n ω ω ω. So xt et2 cos 11 t2 1 11 sin 11 t2 12 et2 11 cos 11 t2 φ where φ tan11 11. Now If δ 1 the two roots s 1 and s 2 are real and we have an over damped system. Calculate damping factor ζ ζ from overshoot OS O S or decay ratio DR D R. Xt K1t exp s1t K2 exp s2t. The pole locations of the classical second-order homogeneous system d2y dt2 2ζωn dy dt ω2 ny0 13 described in Section 93 are given by p1p2 ζωn ωn ζ2 1.
In a system whose transfer function having the highest power of s equal to 2 in its denominator is called the second order control system. Underdamped second order systems may resonate or oscillate at a greater magnitude than the input M 1. Underdamped case results in complex numbers This generates a decaying oscillating case. For a second order system damping ratio 𝜉𝑖 0. Second order impulse response Underdamped and Undamped Unstable Faster response Slower response Higher frequency oscillations Lower frequency oscillations. Underdamped Second Order Systems. S1 s2 ζωn j ωn1 ζ2.
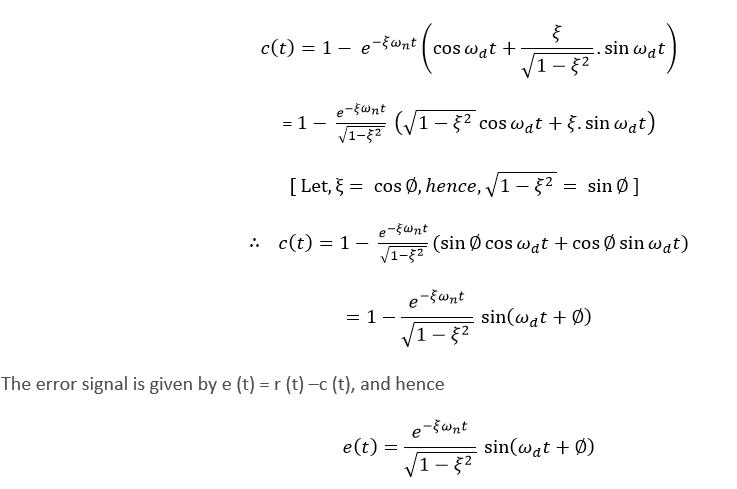
Post a Comment for "Underdamped Second Order System"